Laplace

 Transformada de Laplace

¿Qué es la transformada de Laplace?

La transformada de Laplace ha sido en los últimos años de gran importancia en los estudios de ingeniería, matemática, física, entre otras áreas científicas, ya que además de ser de gran interés en lo teórico, proporciona una forma sencilla de resolver ecuaciones diferenciales, transformándolas en ecuaciones algebraicas.

Originalmente la transformada de Laplace fue presentada por Pierre-Simon Laplace (1745-1827) en su estudio sobre la teoría de la probabilidad, y en principio fue tratada como un objeto matemático de interés meramente teórico.

Las aplicaciones actuales surgen cuando diversos matemáticos trataron de dar una justificación formal a las “reglas operacionales” usadas por Oliver Heaviside (1850-1925) en el estudio de ecuaciones de la teoría electromagnética.

Definición de la transformada de Laplace

Sea f una función definida para t ≥ 0. La transformada de Laplace se define como sigue:

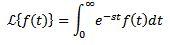
Se dice que la transformada de Laplace existe si la integral anterior converge, en caso contrario se dice que la transformada de Laplace no existe.

Por lo general, para denotar la función que se desea trasformar se usan letras minúsculas y la letra mayúscula corresponde a su transformada. De esta manera tendremos:

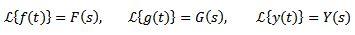
Ejemplos

Considere la función constante f(t) = 1. Tenemos que su transformada es:

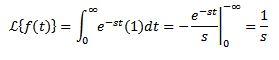
Siempre que la integral converja, es decir, siempre que s > 0. En caso contrario, s < 0, la integral diverge.

Sea g(t)=t. Su transformada de Laplace viene dada por:

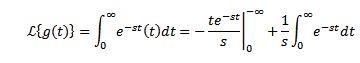
Al integrar por partes y sabiendo que te-st tiende a 0 cuando t tiende a infinito y s > 0, junto con el ejemplo anterior tenemos que:

La transformada puede o no existir, por ejemplo para la función f(t) = 1/t, la integral que define su transformada de Laplace no converge y por lo tanto su transformada no existe.

Las condiciones suficientes para garantizar que la transformada de Laplace de una función f exista, son que f sea continua por partes para t ≥ 0 y sea de orden exponencial.

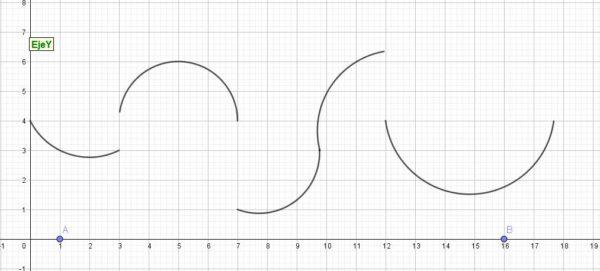
Se dice que una función es continua por partes para t ≥ 0, cuando para cualquier intervalo [a, b] con a > 0, hay un número finito de puntos tk, en donde f tiene discontinuidades y es continua en cada subintervalo [tk-1,tk].

Por otro lado, se dice que una función es de orden exponencial c si existen constantes reales M > 0, c y T > 0 tal que:

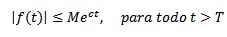
Como ejemplos tenemos que f(t) = t2 es de orden exponencial, ya que |t2| < e3t para todo t > 0.

De manera formal tenemos el siguiente teorema:

Teorema (Condiciones suficientes para la existencia)

Si f es una función continua por parte para t > 0 y de orden exponencial c, entonces existe la transformada de Laplace para s > c.

Es importante resaltar que esta es una condición de suficiencia, es decir, que podría darse el caso de que exista una función que no cumpla dichas condiciones y aun así su transformada de Laplace exista.

Un ejemplo de esto es la función f(t) = t-1/2 que no es continua por partes para t ≥ 0 pero su transformada de Laplace existe.

Transformada de Laplace de algunas funciones básicas

En la siguiente tabla se muestran las transformadas de Laplace de las funciones más comunes.